Polya said it well: “When you have satisfied yourself that the theorem is true, you start proving it.”
开头的话意思是，“当你坚信一个理论是正确的时候，再开始尝试证明它“。这句话里隐藏了一个很重要的观点，数学理论在很多时候的作用是去证明你已有的想法，而不是通过理论推导获取到新的想法。
今天我们要说的旋转位置编码（RoPE, Rotary Position Embedding），以及它的前导工作复数位置编码（Complex Position Embedding），或许就是这种观点的2个实践例子。如果你首先看到的是它们发表出来的数学公式，你可能会没有耐心看完，所幸它们的代码实现并不难，就算弄清楚它们的原理对实际使用并没有什么帮助。但可惜的是，你也会失去了2次为精妙的idea拍手称赞的机会。
RoPE包括复数位置编码，这2者背后的想法都是非常简单且直观的，但是它们相关的理论推导又是平凡且枯燥的。这也正是数学的奇妙之处，论抽象，没有什么事物能比得过它。但学习数学的精髓，就是掌握它的这种抽象，如果数学只是死记硬背的公式，不好意思，它并不是什么神秘的咒语，不会给你带来一丝丝魔力。所以我们今天用简单的语言说明一下它们背后的观点。
什么是复数
因为这2个工作都是建立在复数理论之上，所以我们要耐着性子看一下复数的本质。还好，虽然复数的名字是“复杂的数（Complex number）”，但它的本质是将事情变得简单，不得不说是一次起名上的重大失误。
在有理数还只有正数的年代（1700s），人们并不会理解负数有什么实际意义。今天人们对复数也有着同样的误会，它的本质是旋转。试想有一个有理数的数轴上，1乘以-1表示在数轴上逆时针翻转180°，那么有没有一个数能让$1\times x \times x=-1$，即施加2次使得1进行翻转呢，那就是逆时针翻转90°，这就是$i$的直观理解。
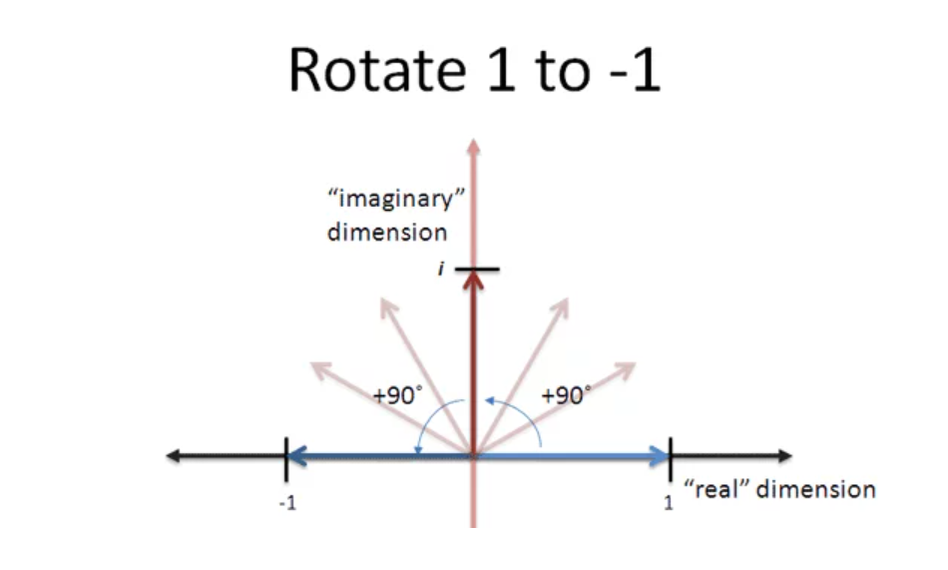顺着这个想法，正常的指数增长是指固定增长率下的持续增长，那么复指数表示固定速率下的持续旋转。欧拉公式$e^{i\pi}=-1$表示将一个数持续旋转弧度$\pi$的情况下，它将指向相反的方向。
在物理中复指数还用来表示正弦信号，因为正弦信号的来源也是旋转运动。
复数位置编码
不同于RNN、CNN等模型，对于Transformer模型来说，位置编码的加入是必不可少的，因为纯粹的Attention模块是无法捕捉输入顺序的，即无法区分不同位置的Token。为此我们大体有两个选择：1、想办法将位置信息融入到输入中，这构成了绝对位置编码的一般做法；2、想办法微调一下Attention结构，使得它有能力分辨不同位置的Token，这构成了相对位置编码的一般做法。
来自 让研究人员绞尽脑汁的Transformer位置编码 - 科学空间|Scientific Spaces (kexue.fm)
以上内容概括了位置编码的作用，以及2大类：绝对位置编码、相对位置编码。但是总体来说都是在一个框架里，即将绝对位置或者相对位置当做一个token，对应1个固定的多维向量，即位置编码。
复数位置编码使用了一种巧妙的视角将文字编码和位置编码融为一体，即将文字向量的每一个维度看成1个正弦信号，所以每个文字的embedding就是由N个幅度、初始相位、频率各不相同的信号组成，信号的横轴就是文字所处的位置编号。虽然单一的正弦信号是有周期的，但是N个正弦信号的组合可以使公共周期变得非常大，也就是这种信号可以表示非常长的距离信息。
用信号集合表示位置编码还有2个显而易见的好处：
- 位置无关的平移特性：任意2个位置之间的转换，即每个信号以各自的速率转动相同的时间，这个转换本身与文字当前所处的位置无关；
- 有界性：正弦信号是上下界的，这点对网络的训练稳定至关重要。
需要说明的是，把信号当做复数位置编码的背后逻辑是我个人的理解，原论文中只有数据理论与证明。
旋转位置编码
“两个二维向量的内积，等于把它们当复数看时，一个复数与另一个复数的共轭的乘积实部。”
来自 让研究人员绞尽脑汁的Transformer位置编码 - 科学空间|Scientific Spaces (kexue.fm)
旋转位置编码的理解需要基于一个抽象：如果将二维向量看做复数，那么向量内积相当于一个复数的角度减去另一个复数的角度，并将它们的模相乘。
上述抽象基于2个事实：
- 复数相乘的含义：1. 模相乘；2. 角度相加；
- 复数的共轭：指模相同，但是角度相反的复数。
这2个向量在Attention计算中分别代表了Q和K，首先在内积之前对这2个向量进行旋转，旋转角度大小与位置成正比关系。那么在做self-attention的时候，基于前面所说的抽象本质，内积的信息里面包含了Q和K的旋转角度之差，这个差是只依赖于位置差的，所以满足位置无关的平移特性。
那么在多维的情况下，可以把embedding看作多组复数的组合，这种类比依然适用。
总结
虽然不能说RoPE是从复数位置编码衍生出来的，因为设置更加巧妙更加简洁，但是这种近乎于直觉的想象力+严密的推理 似乎是它们共同的风格。
数学一定要有直观的意义吗，我认为是的。虽然并不是所有的数学发现都是从实际出发而得来的，但是最终它们一定会用来解决实际的问题。如果没有了这种直观的想象力，那么仅仅从公式推理去做研究，就如同水木失去本源难以发展，又如空中楼阁难以稳固。