MoE指的是sparse mixture of experts,sparse表示推理的时候不是所有的参数都会被激活。通常情况下MoE被认为是一种scaling up模型的技术,使用同样的资源训练更大的模型,某些设定下其效果甚至可能达到与同样参数量稠密网络相当的水平(Deepseek MoE 2B,见论文)。
最近社区里有很多MoE的开源工作,xAI发布了300B的MoE模型,苹果发布了MoE的多模态模型。不禁让人想到一个问题,MoE会是AI的未来吗?这是一个很难回答的问题,从我个人的观点出发,在硬件水平不出现巨大飞跃的前提下,答案是肯定的(Quantum come to recue… i’m waiting)。一方面是因为我相信处在最前沿的模型规模还会呈现大幅的提升,需要有技术来弥补硬件水平和扩大后模型规模之间的差距,而MoE是这方面一项成熟同时具有进一步提升潜力的方法。另外一方面,从神经元活动的分布的角度来看,人脑某些区域也是稀疏的,在进化论的角度也可以被看成一种减少能量消耗的方法。再说一下为什么MoE不会是未来,首先在MoE架构理论中有很多的漏洞,比如训练中需要用辅助loss保持exert激活的均匀性,路由训练过程中会震荡。虽然这些问题都有对应的方法去解决,但这种缝缝补补的技术带来收益的同时也限制了收益的上限(MoE的scaling law中可以体现)。
但这篇博客并不是为了讲MoE技术本身,而是解析一下megatron是如何实现MoE的训练的,以及大规模的MoE模型如何进行并行,同时增加对megatron的了解。
MoE结构回顾
首先,看一下在最主流的transformer框架里,MoE的结构如下图所示:
%%{ init: { 'flowchart': { 'curve': 'bumpX' } } }%%
graph LR
x["X(n-1)"] --> p1["."] --> input_ln["Layer Norm"]
input_ln --> attn["Self Attention"]
attn --> plus1((+))
p1 --> plus1
plus1 --> p2["."] --> attn_ln["Layer Norm"]
subgraph MoE Layer
expert1["Expert 1"]
expert2["Expert 2"]
expert_dot["..."]
expertk["Expert K"]
end
attn_ln -.-> expert2["Expert 2"]
attn_ln --> expert1["Expert 1"]
attn_ln -.-> expert_dot["..."] & expertk["Expert K"]
expert1 --> plus((+))
plus --> plus2((+))
expert2 & expert_dot & expertk -.-> plus((+))
plus2 --> x2["X(n)"]
p2 --> plus2
classDef nodeNoBorder fill:#ffffff,stroke:#000000,stroke-width:0px;
class expert_dot nodeNoBorder
class x nodeNoBorder
class x2 nodeNoBorder
class p1 nodeNoBorder
class p2 nodeNoBorder
class plus nodeNoBorder
class plus1 nodeNoBorder
class plus2 nodeNoBorder
大多数情况下,MoE层是应用在MLP中的,也就是每个expert代表了一个MLP层。MoE并没有引入新的层,除了一个Router Network用来计算token和expert之间的匹配分数。
看起来MoE模型实现上和稠密网络并没有太大的区别,从计算流程上来看确实是这样,下面介绍一个MoE layer最简单的实现(transformer中的MixtralSparseMoeBlock)的过程:
class MixtralSparseMoeBlock(nn.Module):
def __init__(self, config):
super().__init__()
self.hidden_dim = config.hidden_size
self.ffn_dim = config.intermediate_size
self.num_experts = config.num_local_experts
self.top_k = config.num_experts_per_tok
# gating
self.gate = nn.Linear(self.hidden_dim, self.num_experts, bias=False)
self.experts = nn.ModuleList([MixtralBlockSparseTop2MLP(config) for _ in range(self.num_experts)])
def forward(self, hidden_states: torch.Tensor) -> torch.Tensor:
""" """
# 计算routing score
router_logits = self.gate(hidden_states)
routing_weights = F.softmax(router_logits, dim=1, dtype=torch.float)
# 根据topk选出每个token对应的激活专家
routing_weights, selected_experts = torch.topk(routing_weights, self.top_k, dim=-1)
routing_weights /= routing_weights.sum(dim=-1, keepdim=True)
final_hidden_states = []
# 在每个expert上计算选中的token
for expert_idx in range(self.num_experts):
expert_layer = self.experts[expert_idx]
current_state = select_tokens(hidden_states, selected_experts)
if current_state.shape[0] == 0:
continue
# 计算expert的输出
current_hidden_states = expert_layer(current_state) * routing_weights[top_x, idx, None]
final_hidden_states.append(current_hidden_states)
# 重组得到最后输出
final_hidden_states = concat(final_hidden_states, selected_experts)
return final_hidden_states, router_logits
注:这里省略了一些不必要的计算细节,只保留对过程理解有用的部分。比如:select_tokens,concat是为了简化而虚构的函数。
上面的实现方法将所有的expert都加载到显存中,并且在计算expert的时候使用串行的方式。显然因为每个token计算的时候并不会激活所有的expert,虽然在实际训练的过程中每次的输入里包含很多个token,也就是可以保证不会有完全空闲的expert。但是expert上的计算压力明显要低于网络中其余部分,从而造成资源浪费。另外,在实际推理部署的时候,expert往往是分布在不同的设备上的,这就涉及多机通讯的问题。并且,router往往还要考虑负载均衡的问题。这些问题都给实现MoE的过程中增加了困难,下面看megatron是如何解决这些问题的。
这里分为3大块去分析整个实现过程,首先是expert的并行方式,其次是Router的设计,最后是Dispatcher。
Expert Parallel
EP(Expert Parallel)是MoE特有的并行方式,其核心是将expert在多个DP模型副本之间共享,从而实现节约显存的目的。可以说没有EP,那么大规模的MoE模型训练是完全不可能实现的。在介绍EP的划分方式之前,我们先来看一下megatron中并行组的划分方式。
Megatron中常规通讯组划分
首先我们来说一下没有EP的时候通讯组是怎么划分的。megatron中有TP,PP,DP的3种并行方式,这3种并行方式对应的通讯量大小排序是:TP>DP>PP。而在GPU集群里,设备内部的通讯带宽远大于设备间的带宽。因此通讯组划分原则就是,尽量让TP和DP通讯发生在设备内部,而PP组进行跨设备通讯。
如果不太理解这个分配方式,可以直接看下面这个例子。我会在示意图里面标记出每个GPU对应的TP DP PP的组,以及上面存放了对应模型的那部分结构。PS:顺便提一下,megatron中的并行组划分代码在写的时候应该是没有考虑可读性,如果想更快的看懂这块代码,在看之前最好也画一个这样的图对照着。
假设,现在有2台8卡的A100机器,需要训练一个8层的transformer模型,并行设置TP=2,PP=4,DP=2。那么示意图如下:
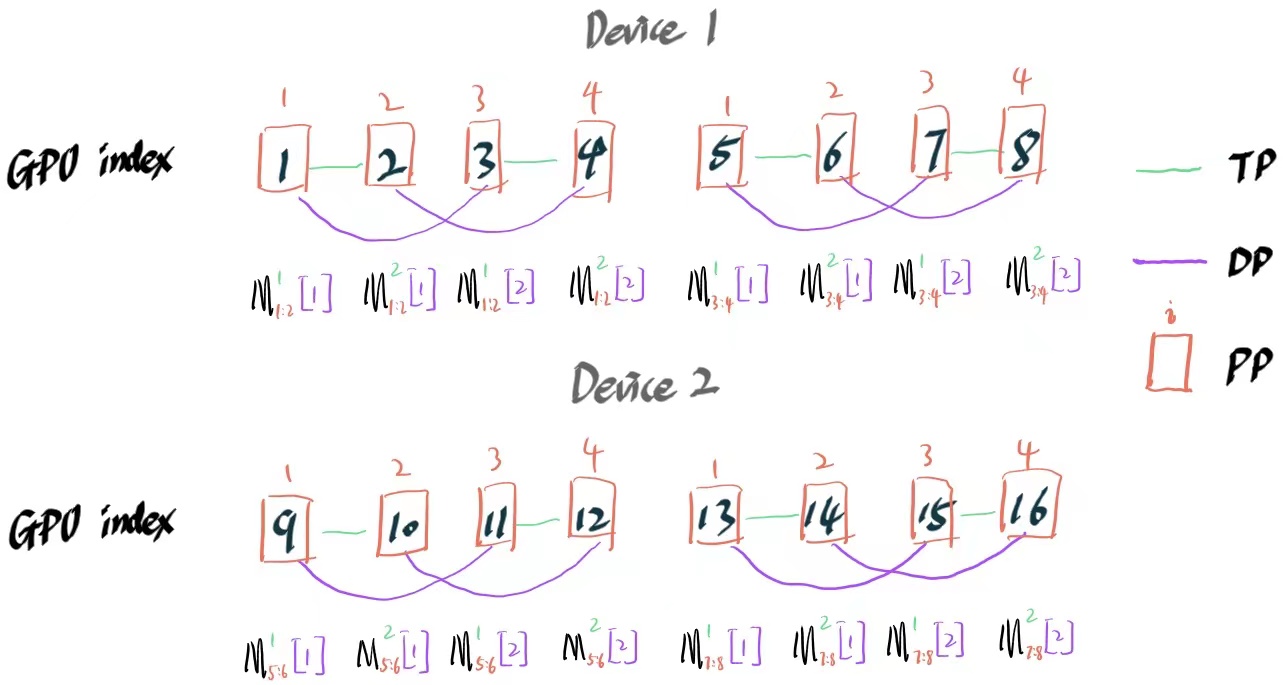
notions*说明:
- $M_{1:8}^1[1]$,下标表示模型的1~8层参数,上标表示TP的第一个参数切片,方括号里表示第一个模型副本。
事实上,PP组的第一个节点和最后一个节点还需要保存embedding和unembedding的矩阵,这里为了方便省略掉了。
MoE layer通讯组划分
通过上面这个例子我们知道了正常的Dense模型在并行情况下是如何切分的,那如果是MoE模型会是怎么样的呢?我们把上一个例子稍微改动一下,把Dense改为MoE模型,每一层transformer里面有8个expert。设置EP=2,意味着每2个模型副本间共享一个完整的MoE层。
我们以1:2层为例,看一下expert会如何进行保存,为了方便我们用一个表格说明。因为PP=4,所以前2层的参数会存放在第1到4个节点上面,因此我们只列出这4个节点,以及节点上面存放的模型参数和expert参数。
| 节点 | 模型参数 | expert参数 |
|---|---|---|
| 1 | $M^1_{1:2}[1]$ | $Experts_{1:4}^1$ |
| 2 | $M^2_{1:2}[1]$ | $Experts_{1:4}^2$ |
| 3 | $M^1_{1:2}[2]$ | $Experts_{5:8}^1$ |
| 4 | $M^2_{1:2}[2]$ | $Experts_{5:8}^2$ |
notions*说明:
- $Experts_{1:4}^1$中,下标表示第1~4个expert对应的参数,上标表示TP的第1个切片。
那么在EP并行的情况下,设备之间的通讯需求分为下面2个部分:
token分发;
通过上面表格可以看到,节点1-4共享一套完整的expert参数。(1, 2), (2, 3)是2个TP组,意味着这2个节点上的数据是相同的。但因为sequence parallel的存在,组内会在sequence方向上进行拆分输入。(1, 2)和 (2, 3)这2个组之间分别组成DP组,所以输入数据是不同的。这也就导致了节点1-4每个节点上面的token都是不一样的,所以在进行路由前,需要把这几个节点上的token都gather起来,再进行全局的分配。
参数更新;
因为EP的存在,expert参数和其他参数的DP组是不一样的,因此,要把存放有相同expert参数的节点放到一个expert独有的DP组里面。
在megatron.core.parallel_state#initialize_model_parallel 中,上面2个组分别对应了变量_TENSOR_AND_EXPERT_PARALLEL_GROUP和_DATA_MODULO_EXPERT_PARALLEL_GROUP。
Router
路由是MoE中最重要的一环,决定了token与expert之间的对应关系。路由方式不光决定了模型的效果,同时也与负载均衡特性息息相关。按照路由的主体可以将路由方式分为3大类,分别是:token-based、expert-based、global assignment,大多数已有的路由方式都可以归纳到这个分类体系下。
%%{ init: { 'flowchart': { 'curve': 'natural' } } }%%
flowchart LR
a["路由方式"]
a --> b["token-based"] & c["expert-based"] & d["global assignment"]
b --> e["hash"] & f["RL"] & g["topK"]
megatron中支持了2种路由方式,分别是TopK和global assignment,下面我们分别介绍2种方法的实现。
global assignment
global assignment将token和expert之间的匹配当做一个全局最优的线性匹配问题,这样做的好处有:1. 在训练过程中,可以做到给每个expert分配相同的token,不需要进行负载均衡;2. 对于routing collapse问题有一定的抑制作用,因为会有token分配到次优的expert上面。
global assignment有很多种不同的解法,通常可能会想到的是Hungarian Algorithm,但是因为其并不能很好利用GPU的并行特点,下面介绍2种对于GPU计算友好的算法。
拍卖行算法
在global assignment第一次被提出的论文《BASE Layers: Simplifying Training of Large, Sparse Models》中,就使用了拍卖行算法作为问题的实现方式。这个算法通过模拟拍卖的过程计算全局最优,在开源框架fairseq中实现了该算法的源码,这里在源码的基础上加了一些必要的注解帮助理解算法的过程。
def balanced_assignment(scores, max_iterations=100):
# scores [8, 80] 8 experts, 80 jobs
num_workers, num_jobs = scores.size()
jobs_per_worker = num_jobs // num_workers
value = scores.clone() # 每个job对每个worker的价值,刚开始出价是0,所以等于scores
iterations = 0
cost = scores.new_zeros(1, num_jobs) # 每个job上面的标价,初始为0
jobs_with_bids = zeros(num_workers).bool() # 每个worker绑定的job数
while not jobs_with_bids.all():
# top_values, top_index [8, 11]
# value表示job对worker的竞标价值:job对worker的价值 - 商品的报价
# 商品的价值初始为0
top_values, top_index = topk(value, k=jobs_per_worker + 1, dim=1)
# worker进行加注
# 加注的量取决于当前job的竞标价值和次优价值之间的差异;
# 显然这种规则可以避免过度的加注
bid_increments = top_values[:, :-1] - top_values[:, -1:] + eps
# 每次下注只下最高的jobs_per_worker个任务,也就是在最理想的情况下,可以一次中标全部
bids = scatter(
zeros(num_workers, num_jobs), dim=1,
index=top_index[:, :-1], src=bid_increments
)
if 0 < iterations < max_iterations:
# If a worker won a job on the previous round, put in a minimal bid to retain
# the job only if no other workers bid this round.
bids[top_bidders, jobs_with_bids] = eps
# Find the highest bidding worker per job
# top_bids, top_bidders [1, 80]
# 中标情况
top_bids, top_bidders = bids.max(dim=0)
jobs_with_bids = top_bids > 0
top_bidders = top_bidders[jobs_with_bids]
# Make popular items more expensive
cost += top_bids # 更新job的标价
value = scores - cost # 更具新的价值,重新计算每个worker和job之间的价值
if iterations < max_iterations:
# If a worker won a job, make sure it appears in its top-k on the next round
# 如果竞标中了,把对应的value设置成无穷大,保证下一轮还会竞标
value[top_bidders, jobs_with_bids] = ∞
else:
value[top_bidders, jobs_with_bids] = scores[top_bidders, jobs_with_bids]
iterations += 1
return top_index[:,:-1].reshape(-1)
如果对该方法感兴趣,在论文《Auction Algorithms for Network Flow Problems: A Tutorial Introductionl》中可以找到收敛到最优点的证明。
sinkhorn算法实现
相比于sinkhorn算法,它的一种特殊例子Wasserstein metric可能更出名一点,大名鼎鼎的WGAN中的W所代表的就是它。Wasserstein metric可以理解为两个不同分布之间的最短距离,同时也是Optimal Transport问题的最优解。
什么是Optimal Transport?我们可以举一个例子:假设你有10个仓库在不同的位置,然后你有5个顾客需要从你这里进货。每个仓库中的货物数量用向量$c\in \mathbf R^{10}$c表示,每个顾客需要的货物用向量$r\in \mathbf R^5$表示,c和r可以被看成2个分布。进货的成本可以被表示为一个矩阵$M \in \mathbf R^{10\times 5}$,同样任意一种进货的方式可以被表示为$P\in \mathbf R^{10\times 5}$。r和c之间的Optimal Transport任务可以看成找到整体成本最小的进货方式$P^*$,并且此时的进货成本可以被看做是Wasserstein metric。
在这个例子中,Optimal Transport的任务可以形式化写成下面这种方式: $$ d(r, c) = \underset{valid\ P}{min} \sum_{i,j}{P_{ij}M_{ij}} $$ sinkhorn算法在此基础上加入P的信息熵作为一个限制项,确保配货方式不会落入极端情况。对应到这面这个例子中,你可能并不想出现所有人都去一个仓库进货的情况。 $$ d^{\lambda}(r, c) = \underset{valid\ P}{min} \sum_{i,j}{P_{ij}M_{ij}} + \frac{1}{\lambda}h(P) $$ 该算法的求解方法如下:
given: $M$, $\mathbf{r}$, $\mathbf{c}$ and $\lambda$ initialize: $P_\lambda = e^{-\lambda C}$ repeat
- scale the rows such that the row sums match $\mathbf{r}$
- scale the columns such that the column sums match $\mathbf{c}$ until convergence
回到MoE的router任务中,token和expert之间的最优匹配可以被看成是在token上的分布与expert上均匀分布之间的最优传输距离。因此可以用sinkhorn求解,但是我们并不关心传输距离,而是可以把行动矩阵$P$看做是一个加了均衡负载约束的喜好分布。
Megatron中使用的sinkhorn主要是为了得到全局最优分配矩阵,因此做了一些简化,与标准实现会有差异。
def sinkhorn(cost: torch.Tensor, tol: float = 0.0001):
"""Sinkhorn based MoE routing function"""
# 这里给的cost其实是logits,代表token和expert之间的匹配程度
cost = torch.exp(cost)
# sinkhorn距离的最优解中的 $\alpha$,$\beta$ 分别是这里的d0和d1
d0 = torch.ones(cost.size(0), device=cost.device, dtype=cost.dtype)
d1 = torch.ones(cost.size(1), device=cost.device, dtype=cost.dtype)
eps = 0.00000001
error = 1e9
d1_old = d1
## 原始分布和目标分布都是均匀分布,所以用1 / d0.size(0) 和 1 / d1.size(0) 表示
while error > tol:
d0 = (1 / d0.size(0)) * 1 / (torch.sum(d1 * cost, 1) + eps)
d1 = (1 / d1.size(0)) * 1 / (torch.sum(d0.unsqueeze(1) * cost, 0) + eps)
error = torch.mean(torch.abs(d1_old - d1))
d1_old = d1
return d1 * cost * d0.unsqueeze(1)
topK
topK的实现与transformers里MixtralSparseMoeBlock的实现类似,根据router输出的logits选出每个token对应的前k个expert,并用softmax计算出对应的prob,作为最终计算结果的调和参数。
代码对应如下:

辅助loss的最佳实现
Router里常见的辅助loss有2种,分别是load-banlance loss和z-loss。前者是为了应对route collapse问题,就是让router的结果更加的均匀,不会出现集中在个别expert上的情况。后者是为了防止gating网络计算的logits过大导致Router收敛变慢的情况。这2个loss都是在gating网络计算的logits上面进行计算得到的,loss的计算方法也没有什么特殊的,只是介绍一下loss生效的方式。
常规的实现方法是将每一个gating网络上面计算的logits收集起来,在模型推理完后计算对应的loss,并加到言模型的交叉熵loss上面。transformers中的switch_transformers就是这样实现的,对应代码如下:
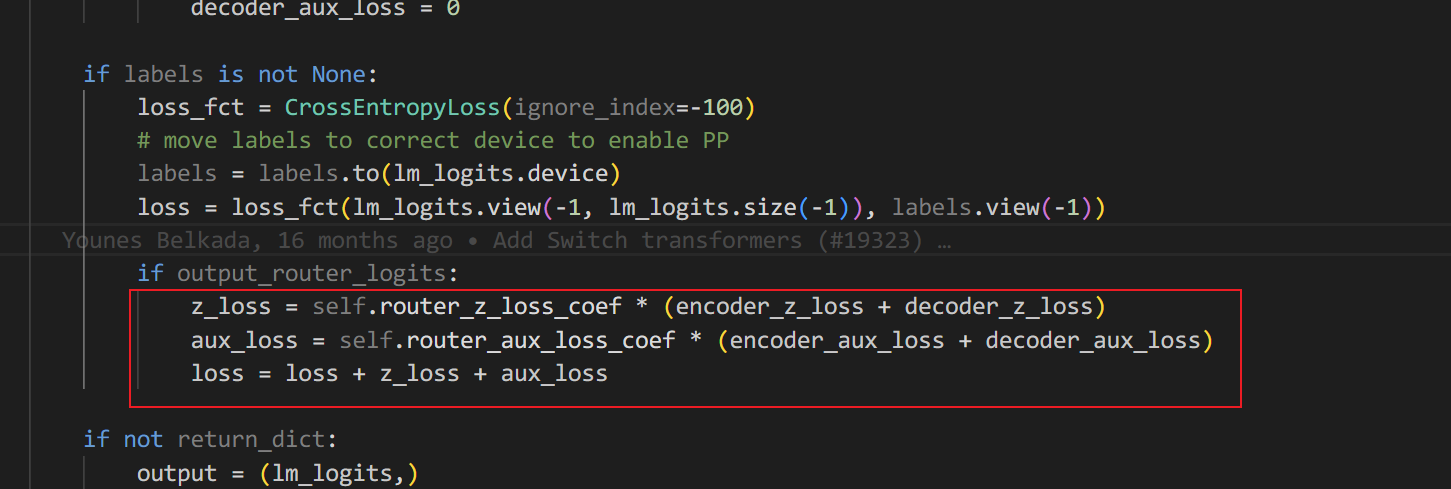
这种方式的问题是如果开启了PP,每个stage都需要将对应的logits传递给下一个stage,当然这样做也没有太多问题。但是megatron里使用了一种更加简洁的方式,给人以耳目一新的感觉。
首先,megatron的实现方式不需要传递中间变量,而是将loss当做网络的一部分。这里我们从megatron中摘抄一段z-loss的实现代码。
def z_loss_func(logits, z_loss_coeff):
z_loss = torch.mean(torch.square(torch.logsumexp(logits, dim=-1))) * z_loss_coeff
return z_loss
class Router(MegatronModule):
...
def apply_z_loss(self, logits):
if self.config.moe_z_loss_coeff is not None:
z_loss = z_loss_func(logits, self.config.moe_z_loss_coeff)
logits = MoEAuxLossAutoScaler.apply(logits, z_loss)
return logits
def forward(self,):
...
logits = self.apply_z_loss(logits)
...
# l
是的,就是这么简单,z_loss_func函数接收logits并返回对应的loss,并且结果中包含了设定好的loss因子。loss并没有被返回并收集,而是直接作为网络的一个计算步骤,所以看起来MoEAuxLossAutoScaler是loss生效的关键。
下面是MoEAuxLossAutoScaler的代码片段:
class MoEAuxLossAutoScaler(torch.autograd.Function):
main_loss_backward_scale: torch.Tensor = torch.tensor(1.0)
@staticmethod
def forward(ctx, output: torch.Tensor, aux_loss: torch.Tensor):
ctx.save_for_backward(aux_loss)
return output
@staticmethod
def backward(ctx, grad_output: torch.Tensor):
(aux_loss,) = ctx.saved_tensors
aux_loss_backward_scale = MoEAuxLossAutoScaler.main_loss_backward_scale
scaled_aux_loss_grad = torch.ones_like(aux_loss) * aux_loss_backward_scale
return grad_output, scaled_aux_loss_grad
@staticmethod
def set_loss_scale(scale: torch.Tensor):
MoEAuxLossAutoScaler.main_loss_backward_scale = scale
看起来也很简单,下面分析一下。MoEAuxLossAutoScaler是一个torch.autograd.Function的类,也就是意味着pytorch可以根据自动微分功能计算对应的梯度。forward函数中接收logits和aux_loss 2个参数,所以backward函数必须返回2个梯度向量,分别对应2个输入。backward函数接收1个向量,因为只有logits参与了后续的计算。backward里做了2件事情,分别是将logits的参数透传给上一个运算,并给aux_loss向量返回一个全是1的梯度,从而使得aux_loss对应的梯度能够传递给前面的运算。
此时有一个问题,学习率是如何生效的呢?注意MoEAuxLossAutoScaler还有一个方法set_loss_scale,这个方法接收一个变量并赋值给静态变量main_loss_backward_scale,这个变量也会和backward中的梯度相乘,显然这个scale的作用就是将学习率传递给梯度。在megatron/core/pipeline_parallel/schedules.py 中调用了这个函数,并将当前的学习率赋值给该静态变量。
Dispatcher
实现过程
在开启EP的情况下,多个DP的模型副本共享一套完整的expert参数,也就是每个模型只有部分expert的参数。所以在计算前需要在多个DP之间重新分配输入数据,以保证每个token都分配到保存有对应expert参数的设备上面。我们还是用刚才的例子来分析一下这个流程,并介绍相应的代码实现和以及变量的含义。
在刚才的例子中,节点 (1,2,3,4) 共享了模型第1~2层上面的experts,具体来说节点(1,2)作为一个完整的TP组保存了前4个expert参数,节点(3,4)保存了后4个expert的参数。
| 节点 | 模型参数 | expert参数 | 输入 |
|---|---|---|---|
| 1 | $M^1_{1:2}[1]$ | $Experts_{1:4}^1$ | $X_1^{0:\frac n 2}$ |
| 2 | $M^2_{1:2}[1]$ | $Experts_{1:4}^2$ | $X_1^{\frac n 2: n}$ |
| 3 | $M^1_{1:2}[2]$ | $Experts_{5:8}^1$ | $X_2^{0:\frac n 2}$ |
| 4 | $M^2_{1:2}[2]$ | $Experts_{5:8}^2$ | $X_2^{\frac n 2: n}$ |
为了方便,我们把前面的表格复制到这里,并添加每个节点上面的输入说明。输入标记$X_1^{0:\frac n 2}$中,下标表示第一个DP组对应的输入,上标表示输入中$[0:\frac n 2]$的子序列,n表示序列的长度。
在每个节点上面all-gather,得到全局的输入;
全局输入为$X_{1:2}^{0:n}=[X_1^{0:\frac n 2}, X_1^{\frac n 2: n},X_2^{0:\frac n 2},X_2^{\frac n 2: n}]$,对应代码中的变量是
global_hidden_states。同样还需要all-gather的有全局的token expert分配矩阵global_indices以及对应的probs矩阵global_probs。筛选出当前节点上面对应的输入,并按照expert index的序号排序;
对应上面例子,节点(1,2)上面分别需要筛选出expert 1到4对应的输入,节点(3,4)上面筛选出expert 4到8对应的输入。本地的输入对应的变量是
local_hidden_states,并且保留global_local_map矩阵用来记录本地输入在global输入中原来的位置。计算expert的结果;
expert推理,得到本地输入对应的输出。计算的过程分为2种,1种是遍历每个expert单独计算,另外一种方式是将所有的expert参数合并起来一次计算,下一节我们会详细讲一下。
将计算完的结果分发到原来的设备上;
通过ReduceScatter的方式完成。
以上过程存在一个问题,既Megatron的实现没有进行token drop。极端情况下所有的token都分配到一个expert上面,会直接导致节点显存崩掉,因此存在一定的不稳定性,但至少效果上面是没有损失的。
通讯量分析
只开启TP和SP的情况下,每一个transformer层需要做4次的all-gather和reduce-scatter,transformer层和MoE层各2次,对应的通讯量为$8D\frac{N-1}{N}$,其中D为hidden层输入的数据量。当开启了EP之后,MoE层的通讯数据由原来的$D$变为$EP\times D$,所以EP的通讯量变为$4(EP-1)D\frac{N-1}{N}$。